第2章 数组

双指针

剑指offerⅡ6：排序数组的两数之和

给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

函数应该以长度为 2 的整数数组的形式返回这两个数的下标值*。*numbers 的下标 从 0 开始计数 ，所以答案数组应当满足 0 <= answer[0] < answer[1] < numbers.length 。

假设数组中存在且只存在一对符合条件的数字，同时一个数字不能使用两次。

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int i = 0, j = numbers.length - 1;
        while (i < j && numbers[i] + numbers[j] != target) {
            if (numbers[i] + numbers[j] > target) {
                j--;
            } else if (numbers[i] + numbers[j] < target) {
                i++;
            }
        }
        return new int[]{i, j};
    }
}

剑指offerⅠ21：调整数组顺序使奇数位于偶数前面

class Solution {
    public int[] exchange(int[] nums) {
        int length = nums.length;
        int i = 0, j = nums.length - 1;
        while (i < j) {
            while (i < j && nums[i] % 2 == 1) {
                i++;
            }
            while (i < j && nums[j] % 2 == 0) {
                j--;
            }
            swap(nums, i, j);
        }
        return nums;
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

剑指offerⅡ7：三数之和

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a ，b ，c *，*使得 a + b + c = 0 ？请找出所有和为 0 且 不重复 的三元组。

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        if (nums.length >= 3) {
            Arrays.sort(nums);
            int i = 0;
            while (i < nums.length - 2) {
                twoSum(i, -nums[i], nums, ans);
                int temp = nums[i];
                while (i < nums.length && nums[i] == temp) {
                    i++;
                }
            }
        }
        return ans;
    }

    private void twoSum(int i, int k, int[] nums, List<List<Integer>> ans) {
        int left = i + 1, right = nums.length - 1;
        while (left < right) {
            if (nums[left] + nums[right] == k) {
                ans.add(Arrays.asList(nums[i], nums[left], nums[right]));
                int temp = nums[left];
                //这种去除重复数字的方法的好处是：第一次必然需要移动一次，否则会陷入死循环
                while (temp == nums[left] && left < right) {
                    left++;
                }
            } else if (nums[left] + nums[right] < k) {
                left++;
            } else if (nums[left] + nums[right] > k) {
                right--;
            }
        }
    }
}

剑指offerⅡ8：大于等于k的最短子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

方法一：自己的方法

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int i = 0, j = 0, sum = 0, min = Integer.MAX_VALUE;
        int length = nums.length;
        sum = nums[0];
        while (j < length) {
            if (sum >= target) {
                min = Math.min(j - i + 1, min);
                sum = sum - nums[i++];
            } else {
                if (j == length - 1)
                    break;
                sum = sum + nums[++j];
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }
}

方法二：书上的写法

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0;
        int sum = 0;
        int minLength = Integer.MAX_VALUE;
        for (int right = 0; right < nums.length; right++) {
            sum = sum + nums[right];
            while (sum >= target && left <= right) {
                int length = right - left + 1;
                minLength = Math.min(length, minLength);
                sum = sum - nums[left++];
            }
        }
        return minLength == Integer.MAX_VALUE ? 0 : minLength;
    }
}

剑指offerⅡ9：乘积小于k的子数组个数

给定一个正整数数组 nums和整数 k ，请找出该数组内乘积小于 k 的连续的子数组的个数。

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        int product = 1;
        int left = 0;
        int ans = 0;
        for (int right = 0; right < nums.length; right++) {
            product = product * nums[right];
            while (product >= k && left <= right) {
                product = product / nums[left++];
            }
            ans = ans + right - left + 1;
        }
        return ans;
    }
}

这个题和面试题8一个套路。

累加数组数字求子数组之和

剑指offerⅡ10：和为k的子数组

给定一个整数数组和一个整数 k **，**请找到该数组中和为 k 的连续子数组的个数。

方法：前缀和+哈希

class Solution {
    public int subarraySum(int[] nums, int k) {
        //键是和，值是和出现的次数
        Map<Integer, Integer> sumToCount = new HashMap<Integer, Integer>();
        sumToCount.put(0, 1);//和为0出现了1次，目的是在index为0的左边定个左边界
        int sum = 0, count = 0;
        for (int num : nums) {
            sum = sum + num;
            count = count + sumToCount.getOrDefault(sum - k, 0);    //1.
            sumToCount.put(sum, sumToCount.getOrDefault(sum, 0) + 1);//2.
            //1和2不能调换顺序，因为要保证j<i
            //否则遇到这种情况[-1,1,0]，target=0时会出现错误
        }
        return count;
    }
}

这个题的核心方法是统计所有以每个位置结尾的和为k的子数组。

当扫描到数组的第i个数字并求得前i个数字之和为x时，需要知道在i之前存在多少个j并且前j个数字之和为x-k，即从j+1到i的和为k。

剑指offerⅡ11: 0和1个数相同的子数组

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

方法：前缀和+哈希 不能用之前的滑动窗口去做，是因为数组中有负值。

class Solution {
    public int findMaxLength(int[] nums) {
        Map<Integer, Integer> sumToIndex = new HashMap<Integer, Integer>();
        sumToIndex.put(0, -1);
        int maxLength = 0, sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum = sum + (nums[i] == 0 ? -1 : 1);//这里要加()
            if (sumToIndex.containsKey(sum - 0)) {
                maxLength = Math.max(maxLength, i - sumToIndex.get(sum - 0));
                //这里不用put进[sum,i],否则会覆盖，要保证存的sum对应的index足够小
            } else {
                //没有sum时，才加入
                sumToIndex.put(sum, i);
            }
        }
        return maxLength;
    }
}

剑指offerⅡ12：左右两边子数组的和相等

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

方法：前缀和

class Solution {
    public int pivotIndex(int[] nums) {
        int sum = 0;
        for (int num : nums) {
            sum = sum + num;
        }
        int leftSum = 0;
        for (int i = 0; i < nums.length; i++) {
            leftSum = leftSum + nums[i];
            if (leftSum - nums[i] == sum - leftSum) {
                return i;
            }
        }
        return -1;
    }
}

剑指offerⅡ13：二维子矩阵的数字之和

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。

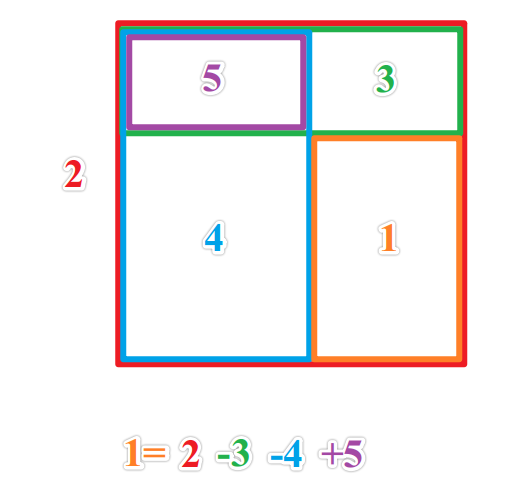
class NumMatrix {
    private int[][] sums;//二维矩阵前缀和

    public NumMatrix(int[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return;
        }
        sums = new int[matrix.length + 1][matrix[0].length + 1];
        for (int i = 0; i < matrix.length; i++) {
            int rowSum = 0;
            for (int j = 0; j < matrix[0].length; j++) {
                rowSum = rowSum + matrix[i][j];
                sums[i + 1][j + 1] = sums[i][j + 1] + rowSum;
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2 + 1][col2 + 1]
                - sums[row1][col2 + 1]
                - sums[row2 + 1][col1]
                + sums[row1][col1];
    }
}